（本小题满分12分）某校对数学、物理两科进行学业水平考前辅导，辅导后进行测试，按照成绩（满分均为100分）划分为合格（成绩大于或等于70分）和不合格（成绩小于70分）．现随机抽取两科各100名学生的成绩统计如下：
| 成绩（单位：分） |
 |
 |
 |
 |
 |
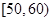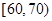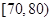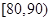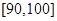| 数学 |
8 |
12 |
40 |
32 |
8 |
| 物理 |
7 |
18 |
40 |
29 |
6 |
（1）试分别估计该校学生数学、物理合格的概率；
（2）设数学合格一人可以赢得4小时机器人操作时间，不合格一人则减少1小时机器人操作时间；物理合格一人可以赢得5小时机器人操作时间，不合格一人则减少2小时机器人操作时间．在（1）的前提下，
（i）记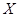
为数学一人和物理一人共同赢得的机器人操作时间（单位：小时）总和，求随机变量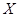的分布列和数学期望；
（ii）随机抽取4名学生，求这四名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于13小时的概率．
是常数），且
（其中
为坐标原点）.
关于
的函数关系式
；
时，
的最大值为4，求
的值.
（
，
）为偶函数，其图象上相邻的两个最高点之间的距离为
．
的解析式；
，
，求
的值．
．
的单调递增取区间；
的图象向左平移
个单位后，再将图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数
的图象，求
的最大值及取得最大值时的
的集合．
，
，且向量
与
不共线.
，求
；
与
互相垂直，求
的值.
终边上一点P（－4，3），求
的值