(13分)动画片《熊出没》中有这样一个情节:某天熊大和熊二中了光头强设计的陷阱, 被挂在了树上,聪明的熊大想出了一个办法,让自己和熊二荡起来使绳断裂从而得救,其过程可简化如图所示,设悬点为0,离地高度为H=6m,两熊可视为质点且总质量m=500kg,重心为A,荡下过程重心到悬点的距离L=2m且保持不变,绳子能承受的最大张力为T=104N,光头强(可视为质点)位于距离0点水平距离s=5m的B点处,不计一切阻力,重力加速度g=10m/s2。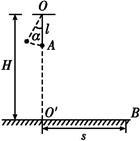
(1)熊大和熊二为了解救自己,荡至最高点时绳与竖直方向的夹角α至少为多大?
(2)设熊大和熊二刚好在向右摆到最低点时绳子断裂,则他们的落地点离光头强的距离为多少?
(3)如果重心A到0的距离可以改变,且两熊向右摆到最低点时绳子恰好断裂,有无可能在落地时砸中光头强?请通过计算说明。
在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚韧不拔的意志和自强不息的精神.为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化.一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示.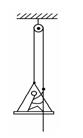
设运动员质量为65 kg,吊椅的质量为15 kg,不计定滑轮与绳子间的摩擦,重力加速度取g=10 m/s2,当运动员与吊椅一起以a=1 m/s2的加速度上升时,试求:
(1)运动员竖直向下拉绳的力;
(2)运动员对吊椅的压力.
如图所示,水平面上放有质量均为m=1 kg的物块A和B(均视为质点),A、B与地面的动摩擦因数分别为μ1=0.4和μ2=0.1,相距L=0.75 m.现给物块A一初速度v0使之向物块B运动,与此同时给物块B一个F=3 N水平向右的力使其由静止开始运动,取g=10 m/s2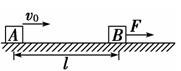
求:
(1)物块B运动的加速度大小;
(2)若要使A能追上B,v0应满足什么条件?
水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37°。水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为μ=0.10。取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6。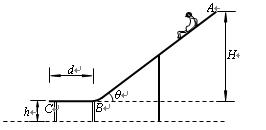
一小朋友从滑梯顶端A点无初速地自由滑下,求:
(1)小朋友沿斜槽AB下滑时加速度的大小a;(2)小朋友滑到C点时速度的大小υ;
一光滑圆环固定在竖直平面内,环上套着两个小球A和B(中央有孔),A、B间由细绳连接着,它们处于如图所示位置时恰好都能保持静止状态。此情况下,B球与环中心O处于同一水平面上,B间的细绳呈伸直状态,与水平线成300夹角。已知B球的质量为m,求细绳对B球的拉力和A球的质量。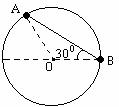
在如图所示的坐标系中,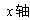 沿水平方向,
沿水平方向,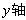 沿竖直方向,第二象限内存在沿
沿竖直方向,第二象限内存在沿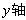 负方向的匀强电场,在第三象限内存在垂直
负方向的匀强电场,在第三象限内存在垂直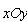 平面(纸面)向里的匀强磁场.一质量为
平面(纸面)向里的匀强磁场.一质量为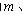 电荷量为
电荷量为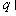 的带正电粒子(不计重力),从
的带正电粒子(不计重力),从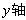 上的
上的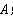 点以
点以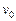 的初速度沿
的初速度沿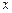 轴负方向进入第二象限之后到达
轴负方向进入第二象限之后到达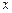 轴上
轴上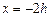 处的
处的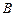 点。带电粒子在
点。带电粒子在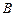 点的速度方向与
点的速度方向与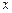 轴负方向成45°角,进入第三象限后粒子做匀速圆周运动,恰好经过
轴负方向成45°角,进入第三象限后粒子做匀速圆周运动,恰好经过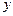 轴上
轴上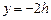 处的
处的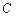 点。
点。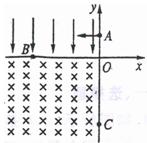
求:
(1)粒子到达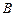 点时速度大小;
点时速度大小;
(2)第二象限中匀强电场的电场强度的大小;
(3)第三象限中磁感应强度的大小和粒子在磁场中的运动时间.