(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)
已知:如图,在平面直角坐标系 中,正比例函数
中,正比例函数 的图像经过点
的图像经过点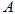 ,点
,点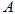 的纵坐标为
的纵坐标为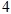 ,反比例函数
,反比例函数 的图像也经过点
的图像也经过点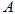 ,第一象限内的点
,第一象限内的点 在这个反比例函数的图像上,过点
在这个反比例函数的图像上,过点 作
作 轴,交
轴,交 轴于点
轴于点 ,且
,且 .
.
求:(1)这个反比例函数的解析式;(2)直线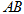 的表达式.
的表达式.
(年山东枣庄10分)如图,一次函数y=ax+b与反比例函数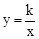 的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为
的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为 ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.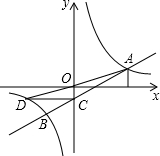
(1)求一次函数与反比例函数的解析式;
(2)求四边形OCBD的面积.
(2014年江苏淮安12分)如图,点A(1,6)和点M(m,n)都在反比例函数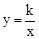 (x>0)的图象上。
(x>0)的图象上。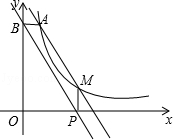
(1)k的值为 ;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
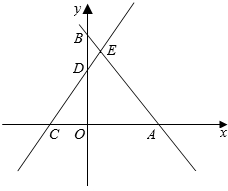
(年黑龙江牡丹江10分)如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2﹣18x+72=0的两根(OA>OC),BE=5,tan∠ABO=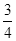 .
.
(1)求点A,C的坐标;
(2)若反比例函数y=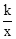 的图象经过点E,求k的值;
的图象经过点E,求k的值;
(3)若点P在坐标轴上,在平面内是否存在一点Q,使以点C,E,P,Q为顶点的四边形是矩形?若存在,请写出满足条件的点Q的个数,并直接写出位于x轴下方的点Q的坐标;若不存在,请说明理由.
(年福建泉州14分)如图,直线y=﹣x+3与x,y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).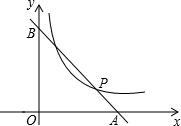
(1)求该反比例函数的关系式;
(2)设PC⊥y轴于点C,点A关于y轴的对称点为A′;
①求△A′BC的周长和sin∠BA′C的值;
②对大于1的常数m,求x轴上的点M的坐标,使得sin∠BMC=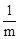 .
.
(2014年江苏徐州10分)如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数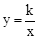 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).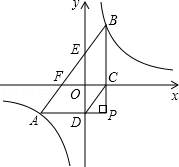
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为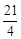 时,求点P的坐标.
时,求点P的坐标.