（.天津市，第24题，10分）（本小题10分）
将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（
，0），点B（0，1），点O（0，0）. 过边OA上的动点M（点M不与点O，A重合）作MN⊥AB于点N，沿着MN折叠该纸片，得顶点A的对应点A′. 设OM =m，折叠后的△A′MN与四边形OMNB重叠部分的面积为S.
（Ⅰ）如图①，当点A′与顶点B重合时，求点M的坐标；
（Ⅱ）如图②，当点A′落在第二象限时，A′M与OB相交于点C，试用含m的式子表示S；
（Ⅲ）当S=
时，求点M的坐标（直接写出结果即可）．
如图是七年级(3)班部分学生的座次表，你能用有序数对表示这些同学的座位情况吗？试试看．
如图，已知正比例函数y＝2x和反比例函数的图象交于点A（m，－2）．
（1）求反比例函数的解析式；
（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；
（3）若双曲线上点C（2，n）沿OA方向平移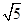
个单位长度得到B，判断四边形OABC的形状并证明你的结论．
如图，已知反比例函数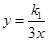
的图象与一次函数y＝k2x＋m的图象交于A（－1，a）、B（
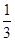，－3）两点，连接AO．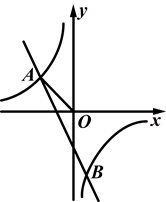
（1）求反比例函数和一次函数的表达式；
（2）设点C在y轴上，且与点A、O构成等腰三角形，请直接写出点C的坐标．
如图，直线y＝k1x＋b与双曲线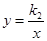
相交于A（1，2），B（m，－1）两点．
（1）求直线和双曲线的解析式；
（2）若A1（x1，y1），A2（x2，y2），A3（x3，y3）为双曲线上的三点，且x1＜x2＜0＜x3，请直接写出y1，y2，y3的大小关系式；
（3）观察图象，请直接写出不等式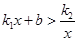
的解集．
已知反比例函数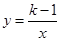
的图象的两个分支分别位于第一、三象限．
（1）求k的取值范围；
（2）若一次函数y＝2x＋k的图象与该反比例函数的图象有一个交点的纵坐标是4．求当x＝－6时，反比例函数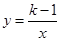的值．