已知集合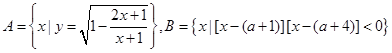 .
.
(1)若 ,求
,求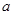 的取值范围;
的取值范围;
(2)若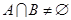 ,求
,求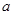 的取值范围.
的取值范围.
(本小题共14分)已知函数 (其中常数
(其中常数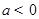 ).
).
(1)求函数 的定义域及单调区间;
的定义域及单调区间;
(2)若存在实数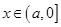 ,使得不等式
,使得不等式 成立,求
成立,求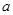 的取值范围.
的取值范围.
(本小题共13分)△ABC的三个内角A,B,C的对边分别为a,b,c,且△ABC的面积为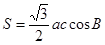 .
.
(1)若 ,求角A,B,C的大小;
,求角A,B,C的大小;
(2 )若a=2,且 ,求边c的取值范围.
,求边c的取值范围.
(本小题共14分)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2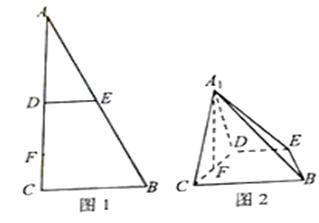
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
(本小题共13分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(1)求上图中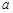 的值;
的值;
(2)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(3)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明)