(本小题满分12分)若函数f(x)=ax2+2x- ln x在x=1处取得极值.
ln x在x=1处取得极值.
(1)求a的值;
(2)求函数f(x)的单调区间及极值.
已知函数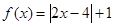 .
.
(Ⅰ)解不等式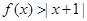 ;
;
(Ⅱ)设正数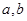 满足
满足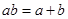 ,若不等式
,若不等式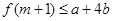 对任意
对任意 都成立,求实数
都成立,求实数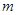 的取值范围.
的取值范围.
已知等比数列 满足2a1+a3=3a2,且a3+2是a2,a4的等差中项.
满足2a1+a3=3a2,且a3+2是a2,a4的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,Sn=b1+b2+…+bn,求使Sn-2n+1+47<0成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn-2n+1+47<0成立的正整数n的最小值.
在 中,内角
中,内角 ,
, ,
, 对应的边分别为
对应的边分别为 ,
, ,
, (
( ),且
),且 .
.
(Ⅰ)求角 ;
;
(Ⅱ)求证: ;
;
(Ⅲ)若 ,且
,且 边上的中线
边上的中线 长为
长为 ,求
,求 的面积.
的面积.
已知 ,函数
,函数 的最小值为4.
的最小值为4.
(Ⅰ)求 的值;
的值;
(Ⅱ)求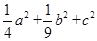 的最小值.
的最小值.
如图,某小区准备在一直角围墙 内的空地上植造“绿地
内的空地上植造“绿地 ”,其中
”,其中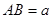 ,
,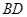 长可根据需要进行调节(
长可根据需要进行调节( 足够长),现规划在
足够长),现规划在 内接正方形
内接正方形 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积 与种花的面积
与种花的面积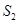 的比
的比 为
为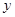 .
.
(1)设角 ,将
,将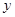 表示成
表示成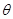 的函数关系;
的函数关系;
(2)当 为多长时,
为多长时,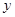 有最小值,最小值是多少?
有最小值,最小值是多少?