(本题6分)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连结AC,CE。
(1)求证:∠B=∠D;
(2)若AB=  ,BC-AC=2,求CE的长。
,BC-AC=2,求CE的长。
化简并求值.
(1)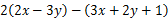 ,其中
,其中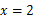 ,
,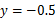 ;
;
(2)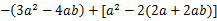 ,其中
,其中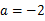 .
.
李强靠勤工俭学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 收入 |
+15 |
+18 |
0 |
+16 |
0 |
+25 |
+24 |
| 支出 |
10 |
14 |
13 |
8 |
10 |
14 |
15 |
(1)到这个周末,李强有多少节余?
(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
为节约用水,某市对居民用水规定如下:大户(家庭人口4人及4人以上者)每月用水15 m3以内的,小户(家庭人口3人及3人以下者)每月用水10 m3以内的,按每立方米收取0.8元的水费;超过上述用量的,超过部分每立方米水费加倍收取.某用户5口人,本月实际用水25 m3,则这户本月应交水费多少元?
某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
-5 |
+7 |
-3 |
+4 |
+10 |
-9 |
-25 |
(1)本周三生产了多少辆摩托车?
(2)本周总生产量与计划生产量相比,是增加还是减少?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
若 >0,
>0, <0,
<0, >
> ,用“<”号连接
,用“<”号连接 ,
, ,
, ,-
,- ,请结合数轴解答.
,请结合数轴解答.