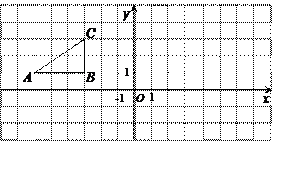已知二次函数 的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围。
分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域,并在每一小
区域内标上数字(如图所示)。欢欢、乐乐两人玩转盘游戏,游戏规则是:同时转动两个转
盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则欢欢胜;若指针所指两区域的
数字之积为偶数,则乐乐胜;若有指针落在分割线上,则无效,需重新转动转盘。
(1)试用列表或画树状图的方法,求欢欢获胜的概率;
(2)请问这个游戏规则对欢欢、乐乐双方公平吗?试说明理由。
已知一元二次方程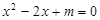 。
。
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为x1,x2,且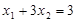 ,求m的值。
,求m的值。
如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4。
(1)求∠POA的度数;
(2)计算弦AB的长。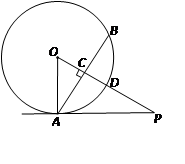
如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点
均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),
点C的坐标为(-3,3)。
(1)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出的图形Rt△A1B1C1的图形,并写出点A1的坐标;
(2)将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形