已知函数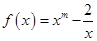 且
且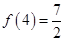 ,
,
(1)求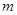 的值;
的值;
(2)判断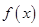 在
在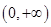 上的单调性,并用定义证明.
上的单调性,并用定义证明.
(3)求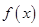 在[ 2 , 5 ]上的值域
在[ 2 , 5 ]上的值域
如图,直角梯形 中,
中,
椭圆 以
以 为焦点且过点
为焦点且过点 ,
,
(1)建立适当的直角坐标系,求椭圆的方程;
(2)若点E满足 是否存在斜率
是否存在斜率 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ,若存在,求
,若存在,求 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
如图,在三棱锥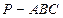 中,
中,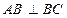 ,
, ,
,
点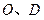 分别是
分别是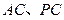 的中点,
的中点,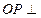 底面
底面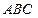 .
.
(1)当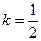 时,求直线
时,求直线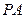 与平面
与平面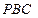 所成角的余弦值;
所成角的余弦值;
(2)当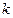 取何值时,
取何值时, 在平面
在平面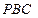 内的射影恰好为△
内的射影恰好为△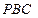 的重心?
的重心?
已知直线与抛物线 交于
交于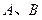 两点,且
两点,且 (
(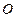 为坐标原点),
为坐标原点), 于点
于点 ,点
,点 的坐标为
的坐标为
(1)求直线 的方程
的方程
(2)抛物线的方程
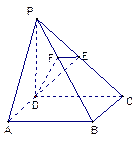
如图,在四棱锥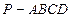 中,底面
中,底面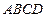 是正方形,侧棱
是正方形,侧棱 底面
底面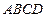 ,
, ,点
,点 是
是 的中点,作
的中点,作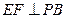 交
交 于点
于点
(1)求证: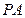 ∥平面
∥平面
(2)求证: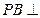 平面
平面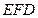
过双曲线 的右焦点
的右焦点 作倾斜角为
作倾斜角为 的直线交双曲线于A、B两点,
的直线交双曲线于A、B两点,
(1)求线段AB的中点C到右焦点 的距离。
的距离。
(2)求线段AB的长。