(本小题满分16分)已知椭圆
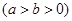 的左、右焦点分别为
的左、右焦点分别为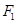 、
、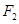 ,短轴两个端点为
,短轴两个端点为 、
、 ,且四边形
,且四边形 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若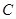 、
、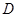 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点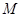 满足
满足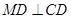 ,连接
,连接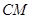 ,交椭圆于点
,交椭圆于点 .证明:
.证明: 为定值.
为定值.
(3)在(2)的条件下,试问 轴上是否存异于点
轴上是否存异于点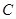 的定点
的定点 ,使得以
,使得以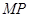 为直径的圆恒过直线
为直径的圆恒过直线 、
、 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知点P的坐标为(3,4,5),试在空间直角坐标系中作出点P.
已知直线l与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l的方程:
(1)过定点A(﹣3,4);
(2)斜率为 .
.
在△ABC中,已知点A(5,﹣2)、B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上.
(1)求点C的坐标;
(2)求直线MN的方程.
(1)求经过点A(﹣5,2)且在x轴上的截距等于在y轴上的截距的2倍的直线方程.
(2)过点A(8,6)引三条直线l1,l2,l3,它们的倾斜角之比为1:2:4,若直线l2的方程是y= x,求直线l1,l3的方程.
x,求直线l1,l3的方程.
△ABC的三个顶点为A(﹣3,0),B(2,1),C(﹣2,3),求:
(1)BC所在直线的方程;
(2)BC边上中线AD所在直线的方程;
(3)BC边上的垂直平分线DE的方程.