(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为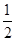 ,双曲线方程为
,双曲线方程为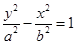 ,直线
,直线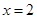 与双曲线的交点为
与双曲线的交点为 且
且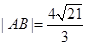 .
.
(Ⅰ)求椭圆与双曲线的方程;
(Ⅱ)过点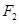 的直线
的直线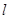 与椭圆交于
与椭圆交于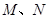 两点,交双曲线于
两点,交双曲线于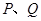 两点,当
两点,当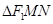 的内切圆的面积取最大值时,求
的内切圆的面积取最大值时,求 的面积.
的面积.
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量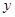 (升)与行驶速度
(升)与行驶速度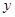 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: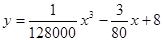 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(1)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的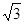 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 交椭圆
交椭圆 于
于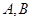 两点,当
两点,当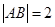 时求直线
时求直线 的方程
的方程
已知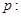 直线
直线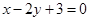 与抛物线
与抛物线 没有交点;
没有交点;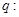 方程
方程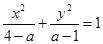 表示椭圆;若
表示椭圆;若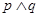 为真命题,试求实数
为真命题,试求实数 的取值范围.
的取值范围.
已知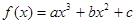 的图象经过点
的图象经过点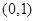 ,且在
,且在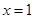 处的切线方程是
处的切线方程是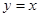
(1)求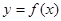 的解析式;(2)求
的解析式;(2)求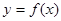 的单调递增区间
的单调递增区间
如图,动点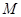 到两定点
到两定点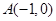 、
、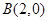 构成
构成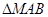 ,且
,且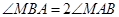 ,设动点
,设动点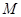 的轨迹为
的轨迹为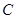 。
。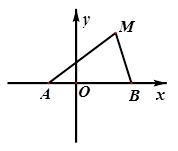
(1)求轨迹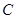 的方程;
的方程;
(2)设直线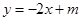 与
与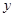 轴交于点
轴交于点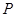 ,与轨迹
,与轨迹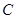 相交于点
相交于点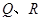 ,且
,且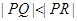 ,求
,求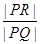 的取值范围。
的取值范围。