如图,在平面直角坐标系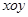 中,已知
中,已知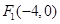 ,
,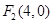 ,
,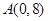 ,直线
,直线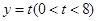 与线段
与线段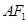 、
、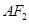 分别交于点
分别交于点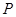 、
、 .
.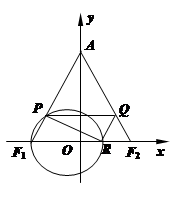
(1)当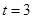 时,求以
时,求以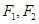 为焦点,且过
为焦点,且过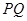 中点的椭圆的标准方程;
中点的椭圆的标准方程;
(2)过点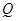 作直线
作直线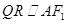 交
交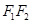 于点
于点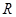 ,记
,记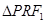 的外接圆为圆
的外接圆为圆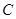 .
.
①求证:圆心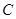 在定直线
在定直线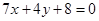 上;
上;
②圆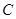 是否恒过异于点
是否恒过异于点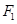 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由.
(本小题满分14分)如图,直三棱柱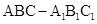 中,
中,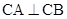 ,
, ,棱
,棱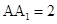 ,
,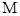 、
、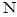 分别是
分别是 、
、 的中点.
的中点.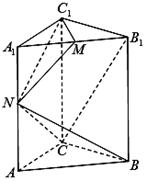
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角
所成角 的正弦值.
的正弦值.
(本小题满分12分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 (个) (个) |
 |
 |
 |
 |
加工的时间 (小时) (小时) |
 |
 |
 |
 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出 关于
关于 的线性回归方程
的线性回归方程 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工 个零件需要多少时间?
个零件需要多少时间?
(本小题满分12分)已知函数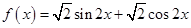 ,
,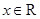 .
.
(1)求 的最大值和最小正周期;
的最大值和最小正周期;
(2)若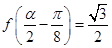 ,
, 是第二象限角,求
是第二象限角,求 .
.
(本小题满分12分)已知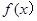 是定义在
是定义在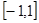 上的奇函数,且
上的奇函数,且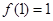 ,当
,当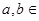
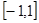 ,
,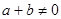 时,有
时,有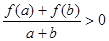 成立.
成立.
(Ⅰ)判断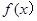 在
在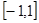 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若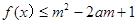 对所有的
对所有的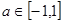 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分12分)已知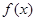 是定义在R上的偶函数,且
是定义在R上的偶函数,且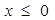 时,
时,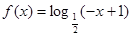 .
.
(Ⅰ)求函数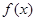 的解析式;
的解析式;
(Ⅱ)若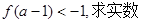
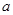 的取值范围.
的取值范围.