(本小题满分12分)已知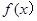 是定义在
是定义在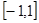 上的奇函数,且
上的奇函数,且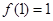 ,当
,当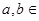
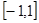 ,
,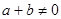 时,有
时,有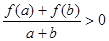 成立.
成立.
(Ⅰ)判断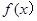 在
在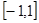 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若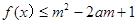 对所有的
对所有的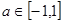 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分10分)已知命题 :函数
:函数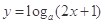 在定义域上单调递增;命题
在定义域上单调递增;命题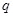 :不等式
:不等式 对任意实数
对任意实数 恒成立,若
恒成立,若 且
且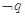 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数 (其中
(其中 是实数).
是实数).
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若设 ,且
,且 有两个极值点
有两个极值点 ,
, (
( ),求
),求 的取值范围.(其中
的取值范围.(其中 为自然对数的底数,
为自然对数的底数, ).
).
(本小题满分12分)数列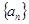 ,
, 的每一项都是正数,
的每一项都是正数,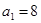 ,
, ,且
,且 ,
,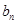 ,
,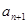 成等差数列,
成等差数列,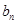 ,
,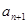 ,
,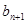 成等比数列,
成等比数列, .
.
(Ⅰ)求 ,
,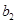 的值;
的值;
(Ⅱ)求数列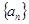 ,
, 的通项公式;
的通项公式;
(Ⅲ)证明:对一切正整数 ,有
,有 .
.
(本小题满分12分)如图,我国南海某处的一个圆形海域上有四个小岛,小岛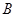 与小岛
与小岛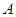 、小岛
、小岛 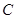 相距都为
相距都为 ,与小岛
,与小岛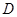 相距为
相距为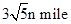 .小岛
.小岛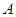 对小岛
对小岛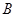 与
与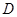 的视角为钝角,且
的视角为钝角,且 .
.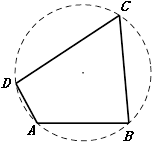
(Ⅰ)求小岛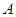 与小岛
与小岛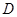 之间的距离和四个小岛所形成的四边形的面积;
之间的距离和四个小岛所形成的四边形的面积;
(Ⅱ)记小岛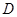 对小岛
对小岛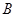 与
与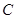 的视角为
的视角为 ,小岛
,小岛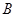 对小岛
对小岛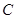 与
与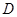 的视角为
的视角为 ,求
,求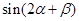 的值.
的值.
(本小题满分12分)已知首项都是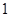 的数列
的数列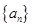 ,
,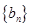
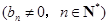 满足
满足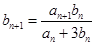 .
.
(Ⅰ)令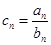 ,求数列
,求数列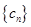 的通项公式;
的通项公式;
(Ⅱ)若数列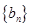 为各项均为正数的等比数列,且
为各项均为正数的等比数列,且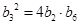 ,求数列
,求数列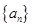 的前
的前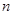 项和
项和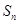 .
.