(本小题满分12分)
在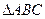 中,角
中,角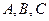 所对的边分别为
所对的边分别为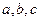 ,满足
,满足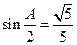 ,且
,且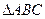 的面积为
的面积为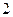 .
.
(1)求 的值;
的值;
(2)若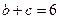 ,求
,求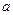 的值.
的值.
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙需维修),其他三面围墙需新建,在旧墙对面的新墙上要留一个宽度为2m的进出口如图所示。已知旧墙的维修费用为45元/m,新墙的造价为180元/m。设利用旧墙的长度为x(单位:m),修建此矩形场地的总费用为y(单位:元)
(1)将y表示为x的函数
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用
解关于x的不等式ax2-(a+1)x+1<0.
数列{an}的前n项和记为Sn,
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且 ,又
,又 成等比数列,求Tn
成等比数列,求Tn
(1)求数列 的通项公式
的通项公式
(2)求数列 的前n项和
的前n项和
已知a= ,c=2,B=150°,求边b的长及
,c=2,B=150°,求边b的长及