(本题满分14分,第1小题满分7分,第2小题满分7分)
为了研究某种癌细胞的繁殖规律和一种新型抗癌药物的作用,将癌细胞注入一只小白鼠体内进行实验,经检测,癌细胞的繁殖规律与天数的关系如下表.已知这种癌细胞在小白鼠体内的个数超过 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.
天数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
癌细胞个数 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
… |
(1)要使小白鼠在实验中不死亡,第一次最迟应在第几天注射该种药物?(精确到1天)
(2)若在第10天,第20天,第30天,……给小白鼠注射这种药物,问第38天小白鼠是否仍然存活?请说明理由.
(本小题12分)函数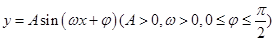 在
在 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当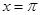 时,
时,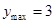 ;当
;当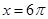 时,
时,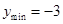 .
.
(Ⅰ)求此函数的解析式;
(Ⅱ)求此函数的单调递增区间.
(本小题10分)命题 :实数
:实数 满足
满足 ,其中
,其中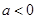 ;命题
;命题 :实数
:实数 满足
满足 或
或 ;若
;若 是
是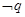 的必要不充分条件,求
的必要不充分条件,求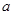 的取值范围.
的取值范围.
已知椭圆 的离心率
的离心率 .直线x=t(t>0)与曲线E交于不同的两点
.直线x=t(t>0)与曲线E交于不同的两点 ,
, ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为 .
.
(1)求椭圆 的方程;
的方程;
(2)若圆 与y轴相交于不同的两点A,B,求△ABC的面积的最大值.
与y轴相交于不同的两点A,B,求△ABC的面积的最大值.
设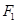 ,
,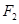 分别是椭圆E:
分别是椭圆E: 的左、右焦点,过
的左、右焦点,过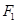 的直线
的直线 与E相交于A、B两点,且
与E相交于A、B两点,且 ,
,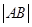 ,
, 成等差数列.
成等差数列.
(Ⅰ)求|AB|;
(Ⅱ)若直线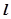 的斜率为1,求b的值.
的斜率为1,求b的值.
(本小题12分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
(1)从频率分布直方图中,估计本次考试成绩的中位数;
(2)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.