（本小题12分）某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成六组后，得到频率分布直方图（如图），观察图形中的信息，回答下列问题．
（1）从频率分布直方图中，估计本次考试成绩的中位数；
（2）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率．
已知方程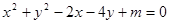
.
（1）若此方程表示圆，求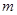
的取值范围；
（2）若（1）中的圆与直线
相交于M，N两点，且OM
ON（O为坐标原点）求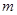的值；
（3）在（2）的条件下，求以MN为直径的圆的方程.
已知正四棱锥（底面是正方形，顶点在底面的投影是底面的中心）P－ABCD如图．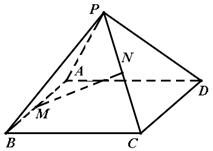
（1）设AB中点为M，PC中点为N，证明：MN//平面PAD.；
（2）若其正视图是一个边长分别为
的等腰三角形，求其表面积S、体积V；
如图，在三棱柱ABC—A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：
（1）B，C，H，G四点共面；
（2）平面EFA1∥平面BCHG.
已知圆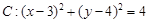
，
（Ⅰ）若直线
过定点
（1，0），且与圆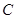
相切，求的方程；
（Ⅱ）若圆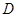
的半径为3，圆心在直线
：
上，且与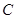圆外切，求圆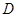的方程．
如图，在平面直角坐标系中，已知平行四边形
的三个顶点坐标：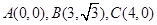
．
（1）求边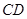
所在直线的方程（结果写成一般式）；
（2）证明平行四边形为矩形，并求其面积．