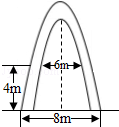
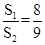吉林省某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距P地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)( )
| A.9.2米 | B.9.1米 | C.9米 | D.5.1米 |
如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数为( )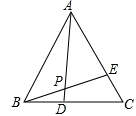
| A.45° | B.60° | C.55° | D.75° |
如图,O是边长为1的正△ABC的中心,将△ABC绕点O逆时针方向旋转180°,得△A1B1C1,则△A1B1C1与△ABC重叠部分(图中阴影部分)的面积为( )
A. |
B.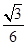 |
C.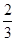 |
D.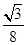 |
如图,P是正△ABC内的一点,若将△PBC绕点B旋转到△P′BA,则∠PBP′的度数是( )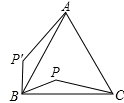
| A.45° | B.60° | C.90° | D.120° |
如图所示,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F,则∠DFC的度数为( )
A.60° B.45° C.40° D.30°
如图,等边三角形ABC的边长为3,D、E分别是AB、AC上的点,且AD=AE=2,将△ADE沿直线DE折叠,点A的落点记为A′,则四边形ADA′E的面积S1与△ABC的面积S2之间的关系是( )
A.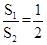 B.
B.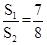 C.
C.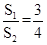 D.
D.