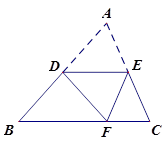
如图,把长为40cm,宽30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余的部分拆成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm(纸板的厚度忽略不计)
(1)长方体盒子的长、宽、高分别为多少?(单位:cm)
(2)若折成的一个长方体盒于表面积是950cm2,求此时长方体盒子的体积.
如图,在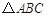 中,
中,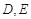 两点分别在
两点分别在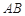 和
和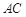 上,求证:
上,求证: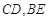 不可能互相平分.
不可能互相平分.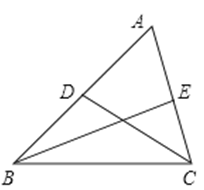
解决下面问题:
如图,在△ABC中,∠A是锐角,点D,E分别在AB,AC上,且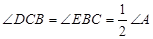 ,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.
,BE与CD相交于点O,探究BD与CE之间的数量关系,并证明你的结论.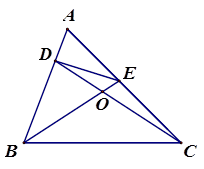
小新同学是这样思考的:
在平时的学习中,有这样的经验:假如△ABC是等腰三角形,那么在给定一组对应条件,如图a,BE,CD分别是两底角的平分线(或者如图b,BE,CD分别是两条腰的高线,或者如图c,BE,CD分别是两条腰的中线)时,依据图形的轴对称性,利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决.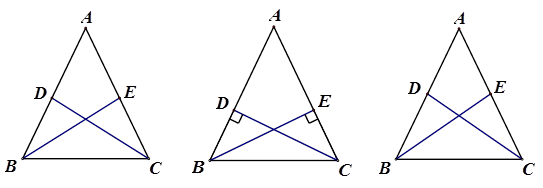
图a图b图c
请参考小新同学的思路,解决上面这个问题..
在平面直角坐标系xoy中,等腰三角形ABC的三个顶点A(0,1),点B在x轴的正半轴上,∠ABO=30°,点C在y轴上.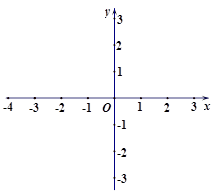
(1)直接写出点C的坐标为;
(2)点P关于直线AB的对称点P′在x轴上,AP=1,在图中标出点P的位置并说明理由;
(3)在(2)的条件下,在y轴上找到一点M,使PM+BM的值最小,则这个最小值为.
列分式方程解应用题
为提升晚高峰车辆的通行速度,北京市交通委路政局积极设置潮汐车道,首条潮汐车道于2013年9月11日开始启用,试点路段为京广桥至慈云寺桥,全程约2.5千米.该路段实行潮汐车道后,在晚高峰期间,通过该路段的车辆的行驶速度平均提高了25%,行驶时间平均减少了1.5分钟.该路段实行潮汐车道之前,在晚高峰期间通过该路段的车辆平均每小时行驶多少千米?
如图,D为AB的中点,点E在AC上,将△ABC沿DE折叠,使点A落在BC边上的点F处.
求证:EF=EC.