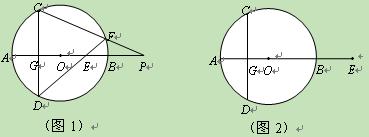
某校部分男生分3组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下.
(1)求训练后第一组平均成绩比训练前增长的百分数;
(2)小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;
(3)你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.
解方程x2﹣4x+1=0.
解不等式组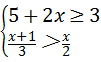 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=-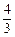 x+
x+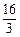 ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
(3)当t为何值时s有最大值?并求出最大值.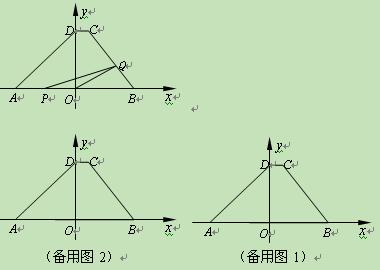
已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.