(本题8分)把下列各数分别填在相应的集合里. ,
, 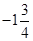 ,
, 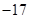 ,
,  ,
, 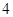 ,
, 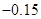 ,
, 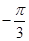 ,
, 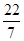 ,
, 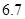 , 0.101001,
, 0.101001, 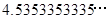 (每两个
(每两个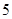 之间依次增加
之间依次增加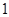 个
个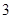 ).
).
整数集合:
 ;
;
分数集合:
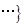 ;
;
无理数集合: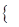
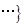 ;
;
负数集合: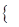
 .
.
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,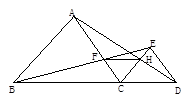
(1)求证:△BCE≌△ACD;
(2)求证:FH//BD.
已知:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.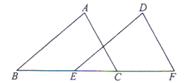
求证:(1)△ABC≌△DEF;(2)BE=CF.
一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是多少?
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x |
… |
﹣2 |
﹣1 |
1 |
2 |
4 |
5 |
… |
| y1 |
… |
﹣5 |
0 |
4 |
3 |
﹣5 |
﹣12 |
… |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
【问题提出】
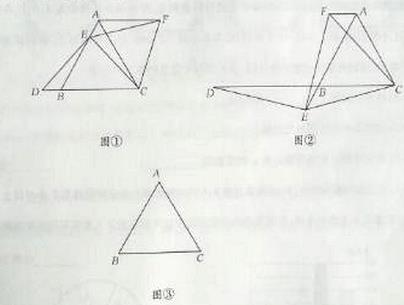
如图①,已知⊿ABC是等边三角形,点E在线段AB上,点D在直线BC上,且DE=EC,将⊿BCE绕点C顺时针旋转 至⊿ACF,连接EF。
至⊿ACF,连接EF。
试证明:AB=DB+AF。
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其它条件不变,线段AB、DB、AF之间又有怎样的数量关系?请说明理由。
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间数量关系,不必说明理由。