(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x |
… |
﹣2 |
﹣1 |
1 |
2 |
4 |
5 |
… |
| y1 |
… |
﹣5 |
0 |
4 |
3 |
﹣5 |
﹣12 |
… |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
如图, 是 的直径,点 是圆上的一点, 于点 , 交 于点 ,连接 ,若 平分 ,过点 作 于点 交 于点 .
(1)求证: 是 的切线;
(2)延长 和 交于点 ,若 ,求 的值;
(3)在(2)的条件下,求 的值.

今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多 元,用 元在甲商店租用服装的数量与用 元在乙商店租用服装的数量相等.
(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用 套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用 套服装,请问在哪家商店租用服装的费用较少,并说明理由.
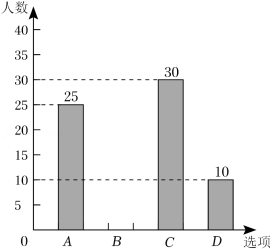
某校将举办的“壮乡三月三”民族运动会中共有四个项目:A跳长绳,B抛绣球,C拔河,D跳竹竿舞.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
|
项目 |
内容 |
百分比 |
|
A |
跳长绳 |
|
|
B |
抛绣球 |
|
|
C |
拔河 |
|
|
D |
跳竹竿舞 |
|
请结合统计图表,回答下列问题:
(1)填空: _____;
(2)本次调查的学生总人数是多少?
(3)请将条形统计图补充完整;
(4)李红同学准备从抛绣球和跳竹竿舞两个项目中选择一项参加,但她拿不定主意,请你结合调查统计结果给她一些合理化建议进行选择.
如图,在 中,点 和点 是对角线 上的两点,且 .
(1)求证: ;
(2)求证: .

如图,在平面直角坐标系中,形如英文字母“ ”的图形三个端点的坐标分别是 .
(1)画出“ ”字图形向左平移 个单位后的图形;
(2)画出原“ ”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)
