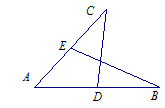
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,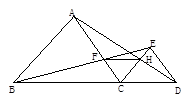
(1)求证:△BCE≌△ACD;
(2)求证:FH//BD.
已知∠MAN,AC平分∠MAN.
(1)在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF,AF相交于P,M.
(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4(第一步)
= y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
| A.提取公因式 | B.平方差公式 |
| C.两数和的完全平方公式 | D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD。若A到河岸CD的中点的距离为500米.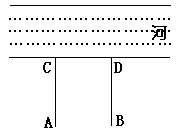
(1)牧童从A处放牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短? 用尺规作图在图中画出来
(2)最短路程是多少?
已知:如图,AB=AC,AE=AD,点D、E分别在AB、AC上.求证:∠B=∠C.