(本小题满分12分)已知函数f(x)=x2-2(a+1)x+2alnx(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间;
(3)若f(x)≤0在区间[1,e]上恒成立,求实数a的取值范围.
(本小题10分)
在边长为60cm的正方形铁皮的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
(本小题9分)
已知复数 ,当实数
,当实数 为何值时,
为何值时,
(1) 为实数;
为实数;
(2) 为虚数;
为虚数;
(3) 为
为 纯虚数.
纯虚数.
(本小题15分)
已知函数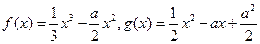 。
。
(I)当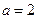 时,求曲线
时,求曲线 在点
在点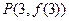 处的切线方程;
处的切线方程;
(Ⅱ)当函数 在区间
在区间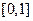 上的最小值为
上的最小值为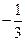 时,求实数
时,求实数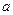 的值;
的值;
(Ⅲ)若函数 与
与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数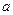 的取值范围。
的取值范围。
(本小题13分)
a,b,c均为实数,且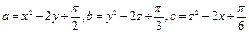 ,求证:
,求证: 中至少有一个大于0.
中至少有一个大于0.
(本小题13分)
实数m取什么值时,复数z=(m2-5m+6)+(m2-3m) 是
是
(1)实数?
(2)虚数?
(3)纯虚数?
(4)表示复数z的点在第二象限?