如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为( ),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
),点B的坐标为(3,0),点C在y轴的正半轴上,且AB=OC.
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
某生姜种植基地计划种植A、B两种生姜30亩.已知A、B两种生姜的年产量分别为
2000千克/亩、2500千克/亩,收购单价分别是8元/千克、7元/千克.
(1)若该基地全年收获A、B两种生姜的年总产量为68000千克,求A、B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A、B两种生姜各多少亩时,全部收购该基地生姜的年总收入最多?最多是多少元?
如图,在△ABC中,点E是AC边上的中点,点F是AB边上的中点,连结EF并延长至点D,再连结BD,请你添加一个条件,使BD=CE(不再添加其它线段,不再标注或使用其他字母), 并给出证明.添加的条件是: ▲.
证明:
(1)计算: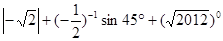 ;
;
(2)先化简,再求值:  ,其中
,其中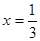 ·
·
(满分14分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DF⊥AC,垂足为点F.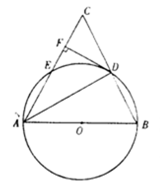
(1)求证:DF是⊙O的切线;
(2)若弧AE=弧DE,DF=2,求弧AD的长.
(满分12分)为了防控甲型H1N1流感,某校积极进行校园环境消毒,购买了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶.(1)如果购买这两种消毒液共用780元,求甲、乙两种消毒液各购买多少瓶?
(2)该校准备再次购买这两种消毒液(不包括已购买的100瓶),使乙种瓶数是甲种瓶数的2倍,且所需费用不多于1200元(不包括780元),求甲种消毒液最多能再购买多少瓶?