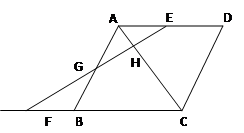如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB中点,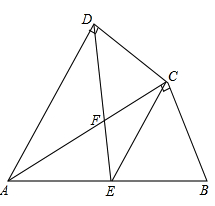
(1)求证:AC2=AB•AD;
(2)若AD=4,AB=6,求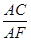 的值.
的值.
(本题13分)已知反比例函数y= (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y= (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式 (用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
(本题12分)如图,ABCD是正方形,BE∥AC,AE=AC,CF∥AE,求证:∠AEB=2∠BCF。
(本题11分) 小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
(1)A点所表示的实际意义是 ;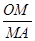 = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
(本题12分)某市实行中考改革,需要根据该市中学生体能的实际情况重新制定中考体育标准.为此,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试.测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少?
(本题7分)如图,在菱形ABCD中,E为AD中点,EF⊥AC交CB的延长线于F.求证:AB与EF互相平分.