(本题12分)已知 是定义在R上的偶函数,当
是定义在R上的偶函数,当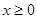 时,
时,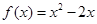
(1)求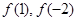 的值;
的值;
(2)求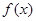 的解析式并画出简图;
的解析式并画出简图;

(3)讨论方程 的根的情况。
的根的情况。
(本小题满分12分)
已知椭圆方程为 ,射线
,射线 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(Ⅰ)求证直线AB的斜率为定值;
(Ⅱ)求△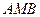 面积的最大值.
面积的最大值.
汽车是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对 排放量超过
排放量超过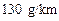 的
的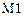 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类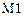 型品牌车各抽取
型品牌车各抽取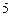 辆进行
辆进行 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: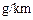 ).
).
| 甲 |
80 |
110 |
120 |
140 |
150 |
| 乙 |
100 |
120 |
 |
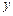 |
160 |
经测算发现,乙品牌车 排放量的平均值为
排放量的平均值为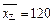
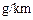 .
.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合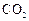 排放量的概率是多少?
排放量的概率是多少?
(Ⅱ)若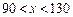 ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车 排放量的稳定性.
排放量的稳定性.
如图,已知四棱锥 ,底面
,底面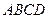 为菱形,
为菱形,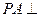 平面
平面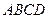 ,
,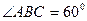 ,
,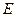 、
、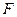 分别是
分别是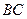 、
、 的中点.
的中点.
(1)判定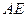 与
与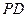 是否垂直,并说明理由。
是否垂直,并说明理由。
(2)设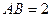 ,若
,若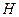 为
为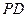 上的动点,若
上的动点,若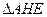 面积的最小值为
面积的最小值为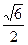 ,求四棱锥
,求四棱锥 的体积。
的体积。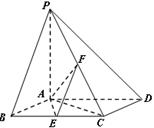
已知数列 的前
的前 项和为
项和为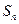 ,且
,且 (
( ).
).
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)若数列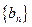 满足
满足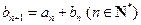 ,且
,且 ,求数列
,求数列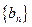 的通项公式.
的通项公式.
在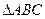 中,内角A,B,C的对边分别是
中,内角A,B,C的对边分别是
(I)求角C的大小;
(II)若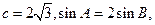 求a,b.
求a,b.