设函数f(x)=ax2+(b-8)x-a-ab的两个零点分别是-3和2.
(1)求f(x)的解析式;
(2)当函数f(x)的定义域是[0,1]时,求函数f(x)的值域.
从集合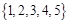 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组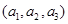 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组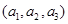 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
设函数f (x) = .
.
(1)求f(x)的最小正周期及其图象的对称轴方程;
(2)将函数f(x)的图象向右平移 个单位长度,得到函数g(x)的图象,求g (x)在区间
个单位长度,得到函数g(x)的图象,求g (x)在区间 上的值域.
上的值域.
设对于任意实数x,不等式|x+7|+|x-1|≥m恒成立.
(1)求m的取值范围;
(2)当m取最大值时,解关于x的不等式|x-3|-2x≤2m-12.
已知等差数列{an}的通项公式为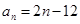 ,从数列{an}中依次取出a1,a2,a4,a8,…,
,从数列{an}中依次取出a1,a2,a4,a8,…, ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.
已知等差数列{an}的前n项的和记为Sn.如果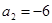 ,
,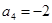
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值;