(本小题满分12分)已知函数 (
( )是偶函数.
)是偶函数.
(1)求k的值;
(2)若函数 的图象与直线
的图象与直线 没有交点,求
没有交点,求 的取值范围;
的取值范围;
(3)若函数 ,
, ,是否存在实数
,是否存在实数 使得
使得 最小值为
最小值为 ,若存在,求出
,若存在,求出 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.
本题满分10分)
已知函数
(1)判断 的单调性并用定义证明;
的单调性并用定义证明;
(2)设 ,若对任意
,若对任意 ,存在
,存在 (
( ),使
),使 ,求实数
,求实数 的最大值.
的最大值.
(本题满分8分)
爱因斯坦提出:“人的差异在于业余时间”.某校要对本校高一学生的周末学习时间进行调查.现从中抽取50个样本进行分析,其频率分布直方图如图所示.记第一组[0,2),第二组[2,4),…,以此类推.
(1)根据频率分布直方图,估计高一段学生周末学习的平均时间;
(2)为了了解学习时间较少同学的情况,现从第一组、第二组中随机抽取2位同学,问恰有一位同学来自第一组的概率.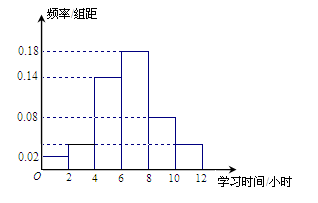
(本题满分7分)
已知 是第三象限角,且
是第三象限角,且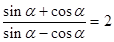 .
.
(1)求 的值;
的值;
(2)设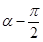 的终边与单位圆交于点
的终边与单位圆交于点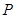 ,求点
,求点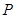 的坐标.
的坐标.
.
设集合 ,
, .
.
(1)求 ;
;
(2)若集合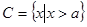 满足
满足 ,求
,求 的取值范围.
的取值范围.
(本题11分)
如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点. (1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的余弦值.(3)求B点到面ECD的距离