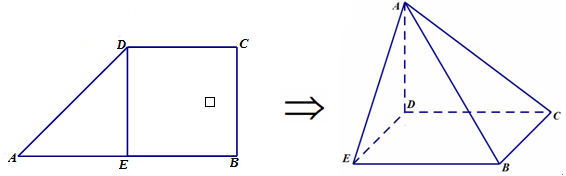
如图,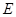 是直角梯形
是直角梯形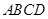 底边
底边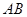 的中点,
的中点, ,将△
,将△ 沿
沿 折起形成四棱锥
折起形成四棱锥 .
.
(1)求证: 平面
平面 ;
;
(2)若二面角 为
为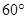 ,求二面角
,求二面角 的正切值.
的正切值.
如图,在三棱锥 中,△
中,△ 和△
和△ 都为正三角形且
都为正三角形且 ,
, ,
, ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,
的中点, 为
为 的中点.
的中点.
(1)求异面直线 和
和 所成的角的大小;
所成的角的大小;
(2)求证:直线 平面
平面 .
.
如图,已知正方形 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
, ,
, 是线段
是线段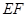 的中点.
的中点.
(1)求三棱锥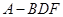 的体积;
的体积;
(2)求 与平面
与平面 所成的角大小.
所成的角大小.
选修4-5:不等式选讲
已知 ,不等式f(x)<4的解集为M.
,不等式f(x)<4的解集为M.
(1)求M;
(2)当 时,证明:
时,证明: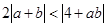 .
.
选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),直线l与曲线
(t为参数),直线l与曲线 交于A,B两点.
交于A,B两点.
(1)求 的长;
的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.