如图所示，一平面框架与水平面成37°角，宽L=0.4m,上、下两端各有一个电阻R0＝1Ω,框架的其他部分电阻不计,框架足够长.垂直于框平面的方向存在向上的匀强磁场,磁感应强度B＝2T。ab为金属杆,其长度为L＝0.4m，质量m＝0.8kg，电阻r＝0.5Ω，金属杆与框架的动摩擦因数μ＝0.5。金属杆由静止开始下滑,直到速度达到最大的过程中,金属杆克服磁场力所做的功为W=1.5J。已知sin37°＝0.6，cos37°=0.8；g取10m／s2.求:
(1)ab杆达到的最大速度v.
(2)ab杆从开始到速度最大的过程中沿斜面下滑的距离.
(3)在该过程中通过ab的电荷量．
如图所示，两带电小球可看作点电荷，QA=3×10－8C，QB=－3×10－8C，A，B两球处于同一水平面，相距L=5cm，在水平方向外电场作用下，A，B保持静止，悬线竖直，求：
（1）A、B两点电荷之间的库仑力的大小
（2）A、B连线中点合场强的大小及方向
半径为r的绝缘光滑圆环固定在竖直平面内，环上套有质量为m、带正电的珠子，空间存在水平向右的匀强电场，如图所示，珠子所受静电力是其重力的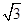
倍。将珠子从环最低位置A点静止释放，求：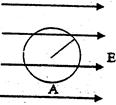
（1）珠子所能获得的最大动能；
（2）最大动能位置圆环对珠子作用力大小；
（3）珠子运动到最高点B点位置。
如图所示，有一初速可忽略的电子经电压U1＝500V加速后，进入两块水平放置、间距为d＝2cm、电压为U2＝10V的平行金属板A、B间。若电子从板正中央水平射入，且恰好能从B板的右端射出.求：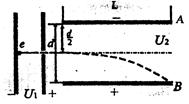
（1）金属板的长度L；
（2）电子离开电场的偏转的角度正切值tanθ;
（3）电子从B板右端射出电场时的动能Ek为多少电子伏特。
如图所示，质量为m的带电粒子以一定的初速度v0由P点射入匀强电场，入射方向与电场线垂直. 粒子从Q点射出电场时，其速度方向与电场线成30°角. 已知匀强电场的宽度为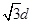
，P、Q两点的电势差为U，不计重力作用，求：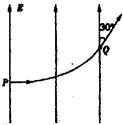
（1）匀强电场的场强大小。
（2）带电粒子的电荷量。
如图，带电小球A、B（可看作点电荷）均用绝缘丝线悬挂点O点。静止时A、B相距为d，小球B的质量为m1，带电荷量为q1。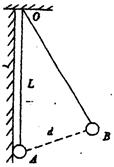
（1）若将B球带电量减到q2，平衡时AB间距离为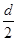
，求q1/q2；
（2）若将B球质量减到m2，平衡时AB间距离为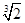
d，求m1/m2.