小明和小芳做配紫色游戏,如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)若出现紫色,则小明胜,否则小芳胜.此游戏的规则对小明、小芳公平吗?试说明理由.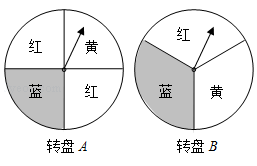
(年四川内江12分)某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
(年江苏扬州12分)某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装,专卖店又缺少资金. “中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示. 该店支付员工的工资为每人每天82元,每天还应该支付其它费用为106元(不包含债务).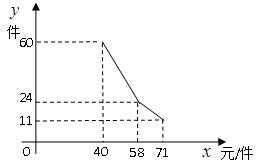
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还债务,当某天的销售价为48元/件时,当天正好收支平衡(收入=支出),求该店员工的人数;
(年湖南怀化10分)设m是不小于﹣1的实数,使得关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x 1,x2.
(1)若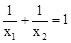 ,求
,求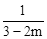 的值;
的值;
(2)求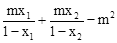 的最大值.
的最大值.
(2014年湖北黄冈9分)某地实行医保制度,并规定:
一、每位居民年初缴纳医保基金70元;
二、居民个人当年看病的医疗费(以定点医院的医疗发票为准,年底按表一的方式结算)报销看病的医疗费用.表一:
| 居民个人当年看病的医疗费用 |
医疗费用报销办法 |
| 不超过n元的部分 |
全部由医保基金承担(即全额报销) |
| 超过n元但不超过6000元的部分 |
个人承担k%,其余由医保基金承担 |
| 超过6000元的部分 |
个人承担20%,其余由医保基金承担 |
设一位居民当年看病的医疗费用为x元,他个人实际承担的医疗费用(包括医疗费用中个人承担的部分和年初缴纳的医保基金)记为y元.
(1)当0≤x≤n时,y=70;当n<x≤6000时,y= (用含n、k、x的代数式表示)
(2)表二是该地A、B、C三位居民2013年看病的医疗费和个人实际承担的医疗费用,根据表中的数据,求出n、k的值.表二:
| 居民 |
A |
B |
C |
| 个人看病所花费的医费用x(元) |
400 |
800 |
1500 |
| 个人实际承担的医疗费用y(元) |
70 |
190 |
470 |
(3)该地居民周大爷2013年看病的医疗费用共32000元,那么他这一年个人实际承担的医疗费用是多少元?
(年黑龙江齐齐哈尔、大兴安岭地区、黑河10分)某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)