已知椭圆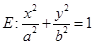
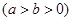 的左焦点为
的左焦点为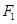 ,右焦点为
,右焦点为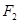 ,离心率
,离心率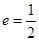 .过
.过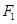 的直线交椭圆于
的直线交椭圆于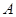 、
、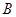 两点,且
两点,且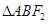 的周长为
的周长为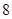 .
.
(1)求椭圆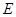 的方程;
的方程;
(2)设动直线 与椭圆
与椭圆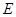 有且只有一个公共点
有且只有一个公共点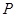 ,且与直线
,且与直线 相交于点
相交于点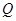 .求证:以
.求证:以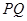 为直径的圆恒过一定点
为直径的圆恒过一定点 .并求出点
.并求出点 的坐标.
的坐标.
(本小题满分12分)在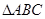 中,已知
中,已知 .
.
(Ⅰ)求sinA与角B的值;
(Ⅱ)若角A,B,C的对边分别为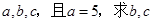 的值.[
的值.[
在自然数列 中,任取
中,任取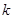 个元素位置保持不动,将其余
个元素位置保持不动,将其余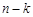 个元素变动位置,得到不同的新数列.由此产生的不同新数列的个数记为
个元素变动位置,得到不同的新数列.由此产生的不同新数列的个数记为 .
.
(1)求 ;
;
(2)求 ;
;
(3)证明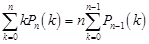 ,并求出
,并求出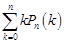 的值.
的值.
(本小题满分10分)如图,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1、BC的中点,点P在直线A1B1上,且满足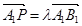 (
(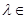 R).
R).
(1)证明:PN⊥AM;
(2)若平面PMN与平面ABC所成的角为45°,试确定点P的位置.
选修4—5:不等式选讲(本小题满分10分)
已知x,y,z均为正数.求证: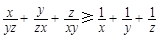 .
.
选修4—4:坐标系与参数方程(本小题满分10分)
已知直线l: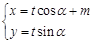 (t为参数)恒经过椭圆C:
(t为参数)恒经过椭圆C: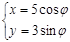 (j为参数)的右焦点F.
(j为参数)的右焦点F.
(1)求m的值;
(2)设直线l与椭圆C交于A,B两点,求 的最大值与最小值.
的最大值与最小值.