(本小题满分12分)
已知 .
.
(Ⅰ)求函数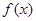 的单调区间;
的单调区间;
(Ⅱ)对一切的 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设函数f (x) = .
.
(1)求f(x)的最小正周期及其图象的对称轴方程;
(2)将函数f(x)的图象向右平移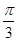 个单位长度,得到函数g(x)的图象,求g (x)在区间
个单位长度,得到函数g(x)的图象,求g (x)在区间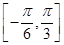 上的值域.
上的值域.
已知 .
.
(1)若a=0时,求函数 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)若函数 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(3)令 是否存在实数a,当
是否存在实数a,当 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是3,若存在,求出a的值;若不存在,说明理由.
的最小值是3,若存在,求出a的值;若不存在,说明理由.
已知 =2,点(
=2,点(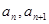 )在函数
)在函数 的图像上,其中
的图像上,其中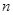 =
= .
.
(1)证明:数列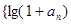 }是等比数列;
}是等比数列;
(2)设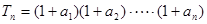 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记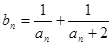 ,求数列{
,求数列{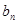 }的前n项和
}的前n项和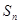 ,并求
,并求 的值.
的值.
在△ABC中,角A、B、C所对的边分别为a、b、c,且cosA=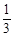 .
.
(1)求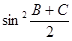
 +cos2A的值;
+cos2A的值;
(2)若a= ,求bc的最大值.
,求bc的最大值.
(1)已知等差数列{an}的公差d > 0,且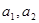 是方程x2-14x+45=0的两根,求数列
是方程x2-14x+45=0的两根,求数列 通项公式(2)设
通项公式(2)设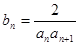 ,数列{bn}的前n项和为Sn,证明
,数列{bn}的前n项和为Sn,证明 .
.