（·辽宁沈阳）如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B的坐标为（60，0），OA=AB，∠OAB=90°，OC=50．点P是线段OB上的一个动点（点P不与点O、B重合），过点P与y轴平行的直线l交边OA或边AB于点Q，交边OC或边BC于点R，设点P横坐标为t，线段QR的长度为m．已知t=40时，直线l恰好经过点C．
（1）求点A和点C的坐标；
（2）当0＜t＜30时，求m关于t的函数关系式；
（3）当m=35时，请直接写出t的值；
（4）直线l上有一点M，当∠PMB+∠POC=90°，且△PMB的周长为60时，请直接写出满足条件的点M的坐标．
解关于x的方程：
＋5x（x－3）＝0．
（本题10分）已知：直角梯形OABC中，BC//OA，∠AO
C＝90°，以AB为直径的OM交OC于点D、E，连结AD、BD．现以O为坐标原点，OA、OC所在直线为x轴、y轴建立如图所示直角坐标系，若抛
物线y＝ax2－2ax－3a(a<0)经过点A、B、D，且B为抛物线的顶点．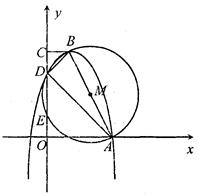
(1)写出顶点B的坐标▲（用a的代数式表示）；
(2)求抛物线的解析式：
(3)在x轴下方的抛物线上是否存在这样的点P：过点P作PN⊥x轴于N，使得△PAN与△OAD相似？若存在，求出点P的坐标：若不存在，说明理由．
（本题8分）如图，AB是⊙O的直径，BC是弦，∠ABC的平分线BD
交⊙O于点D，DE⊥BC，交BC的延长线于点E，RD交AC于点F．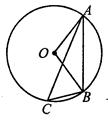
(1)求证：DE是⊙O的切线；
(2)若CE＝2，ED＝4，求⊙O的半径．
（本题8分）某公司投资新建了一商场，共有商铺30间，
据预测，当每间的年租金定为10万元时，可全部租出．每间的年租金每增加5000元，少租出商铺1间．该公司要为租出的商铺每间每年交各种费用1万
元，未租出的商铺每问每年交各种费用5000元． (1)当每间商铺的年租金定为13万元时，能租出多少间？
(2)当每间商铺的年租金定为多少万元时，该公司的年收益（收益＝租金－各种费用）为275万元？
(3)当每间商铺的年租金定为多少万元时，该公司的年收益最大？（假设年
租金每次增加的幅度必须为5000元的倍数）
（本题8分）如图，BD是⊙O的直径，A、C是⊙O上的两点，且AB＝AC，AD与BC的延长线交于点E．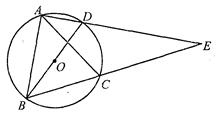
(1)求证：△ABD∽△AEB；
(2)若AD＝1，DE＝3，求BD的长．