(本题8分)如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD
交⊙O于点D,DE⊥BC,交BC的延长线于点E,RD交AC于点F.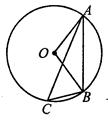
(1)求证:DE是⊙O的切线;
(2)若CE=2,ED=4,求⊙O的半径.
解不等式组: .
计算: .
综合与探究
如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,连接 , .
(1)求 、 , 三点的坐标并直接写出直线 , 的函数表达式.
(2)点 是直线 下方抛物线上的一个动点,过点 作 的平行线 ,交线段 于点 .
①试探究:在直线 上是否存在点 ,使得以点 , , , 为顶点的四边形为菱形,若存在,求出点 的坐标,若不存在,请说明理由;
②设抛物线的对称轴与直线 交于点 ,与直线 交于点 .当 时,请直接写出 的长.

综合与实践
问题情境:数学活动课上,老师出示了一个问题:如图①,在 中, ,垂足为 , 为 的中点,连接 , ,试猜想 与 的数量关系,并加以证明.
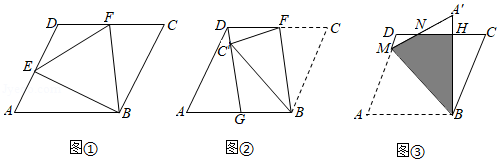
独立思考:(1)请解答老师提出的问题;
实践探究:(2)希望小组受此问题的启发,将 沿着 为 的中点)所在直线折叠,如图②,点 的对应点为 ,连接 并延长交 于点 ,请判断 与 的数量关系,并加以证明.
问题解决:(3)智慧小组突发奇想,将 沿过点 的直线折叠,如图③,点 的对应点为 ,使 于点 ,折痕交 于点 ,连接 ,交 于点 .该小组提出一个问题:若此 的面积为20,边长 , ,求图中阴影部分(四边形 的面积.请你思考此问题,直接写出结果.
某公园为引导游客观光游览公园的景点,在主要路口设置了导览指示牌,某校"综合与实践"活动小组想要测量此指示牌的高度,他们绘制了该指示牌支架侧面的截面图如图所示,并测得 , , , ,四边形 为矩形,且 .请帮助该小组求出指示牌最高点 到地面 的距离(结果精确到 .参考数据: , , , .
