综合与实践
问题情境:数学活动课上,老师出示了一个问题:如图①,在 中, ,垂足为 , 为 的中点,连接 , ,试猜想 与 的数量关系,并加以证明.
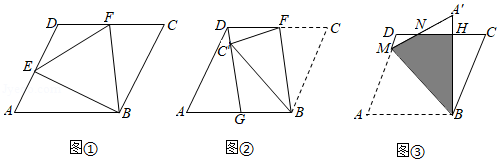
独立思考:(1)请解答老师提出的问题;
实践探究:(2)希望小组受此问题的启发,将 沿着 为 的中点)所在直线折叠,如图②,点 的对应点为 ,连接 并延长交 于点 ,请判断 与 的数量关系,并加以证明.
问题解决:(3)智慧小组突发奇想,将 沿过点 的直线折叠,如图③,点 的对应点为 ,使 于点 ,折痕交 于点 ,连接 ,交 于点 .该小组提出一个问题:若此 的面积为20,边长 , ,求图中阴影部分(四边形 的面积.请你思考此问题,直接写出结果.
已知关于 的一元二次方程 .
(1)求证:无论 为何实数,方程总有两个不相等的实数根;
(2)若方程的两个实数根 , 满足 ,求 的值.
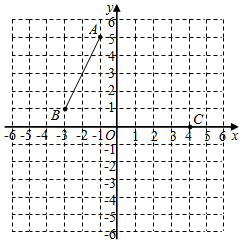
如图,在平面直角坐标系中,已知点 , 和 ,请按下列要求画图并填空.
(1)平移线段 ,使点 平移到点 ,画出平移后所得的线段 ,并写出点 的坐标为 ;
(2)将线段 绕点 逆时针旋转 ,画出旋转后所得的线段 ,并直接写出 的值为 ;
(3)在 轴上找出点 ,使 的周长最小,并直接写出点 的坐标为 .
有4张看上去无差别的卡片,上面分别写有数 ,2,5,8.
(1)随机抽取一张卡片,则抽取到的数是偶数的概率为 ;
(2)随机抽取一张卡片后,放回并混在一起,再随机抽取一张,请用画树状图或列表法,求抽取出的两数之差的绝对值大于3的概率.
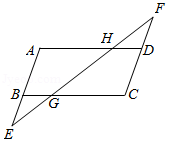
如图,在 中,点 在 的延长线上,点 在 的延长线上,满足 .连接 ,分别与 , 交于点 , .
求证: .
计算: .