（·辽宁锦州）如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
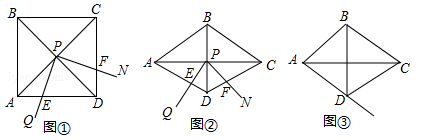
（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是 ；
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=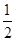
AD，请给出证明；
（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1支钢笔和3本笔记本；小亮用31元买了同样的钢笔2支和笔记本5本。
（1）求每支钢笔和每本笔记本的价格；
（2）校运会后，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出。
已知y=x2＋px＋q，当x=1时，y的值为2；当x=－2时，y的值为2。求x=－3时y的值。
解不等式组，并把解集表示在数轴上
解方程组 （每题6分，共12分）
（1）
（2）
已知抛物线
＝
＋
＋
－4．
（１）当
＝２时，求出此抛物线的顶点坐标；
（２）求证：无论为什么实数，抛物线都与
轴有交点，且经过轴上的一定点；
（３）已知抛物线与轴交于Ａ（1，0）、Ｂ（2，0）两点（Ａ在Ｂ的左边），|1|＜|2|，与轴交于C点，且Ｓ△ABC＝１５．问：过Ａ，Ｂ，Ｃ三点的圆与该抛物线是否有第四个交点？试说明理由．如果有，求出其坐标．