（·辽宁阜新）为了培养学生的阅读习惯，某校开展了“读好书，助成长”系列活动，并准备购置一批图书，购书前，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，根据统计图所提供的信息，回答下列问题：
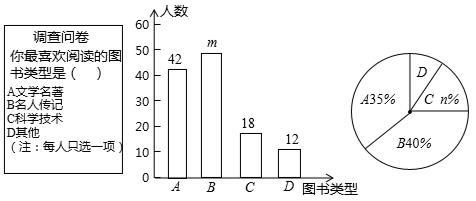
（1）本次调查共抽查了 名学生，两幅统计图中的m= ，n= ．
（2）已知该校共有960名学生，请估计该校喜欢阅读“A”类图书的学生约有多少人？
（3）学校要举办读书知识竞赛，七年（1）班要在班级优胜者2男1女中随机选送2人参赛，求选送的两名参赛同学为1男1女的概率是多少？
反比例函数y=－
与直线y=－x+2的图象交于A、B两点，点A、B分别在第四、二象限，求：
(1)A、B两点的坐标；
(2)△ABO的面积.
如图，第一象限的角平分线OM与反比例函数的图象相交于点A，已知OA=2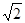
.
（1）求点A的坐标；
（2）求此反比例函数的解析式.
水池中有水若干吨，若单开一个出水口，水流速v与全池水放光所用时t如下表：
| 用时t（小时） |
10 |
5 |
 |
 |
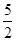2 |
 |
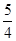1 |
| ——……→逐渐减少 |
|||||||
| 出水速度乙（吨/小时） |
1 |
2 |
3 |
4 |
5 |
8 |
10 |
| ——……→逐渐增大 |
①写出放光池中水用时t（小时）与放水速度v（吨/小时）之间的函数关系.
②这是一个反比例函数吗？
兄弟二人分吃一碗饺子，每人吃饺子的个数如下表：
| 兄（y） |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
…… |
3 |
2 |
1 |
| ——……→逐渐减少 |
||||||||||||
| 弟（x） |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
…… |
27 |
28 |
29 |
| ——……→逐渐增多 |
①写出兄吃饺子数y与弟吃饺子数x之间的函数关系式（不要求写x、y的取值范围）.
②虽然当弟吃的饺子个数增多时，兄吃的饺子数(y)在减少，但y与x是成反例吗？
为什么同一物体早晨的影子较长，中午的影子较短，点燃一只蜡烛，找一木棍变换蜡烛的位置能得出怎样的结论？