如图,两个全等的△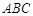 和△
和△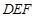 重叠在一起,固定△
重叠在一起,固定△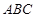 ,将△
,将△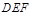 进行如下变换:
进行如下变换:
(1)如图1,△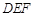 沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出
沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出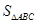 与
与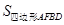 的关系;
的关系;
(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△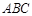 应满足什么条件?请给出证明;
应满足什么条件?请给出证明;
(3)在(2)的条件下,将△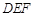 沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出
沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出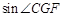 的值.
的值.
如图是某商场第二季度某品牌运动服装的 号, 号, 号, 号, 号销售情况的扇形统计图和条形统计图.
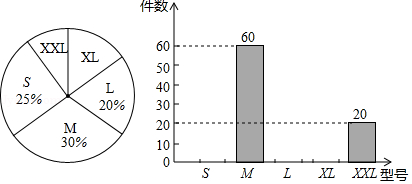
根据图中信息答案下列问题:
(1)求 号, 号运动服装销量的百分比;
(2)补全条形统计图;
(3)按照 号, 号运动服装的销量比,从 号、 号运动服装中分别取出 件、 件,若再取2件 号运动服装,将它们放在一起,现从这 件运动服装中,随机取出1件,取得 号运动服装的概率为 ,求 , 的值.
如图, 中, , 的平分线交 于 , 交 的延长线于点 , 交 于点 .
(1)若 ,求 的度数;
(2)若 ,求 的长.

先化简,再求值: ,其中 , .
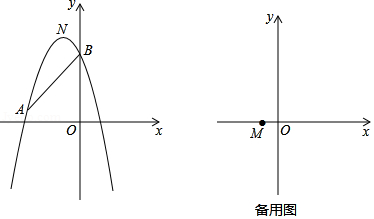
在平面直角坐标系中,抛物线 的顶点为 .
(1)若此抛物线过点 ,求抛物线的解析式;
(2)在(1)的条件下,若抛物线与 轴交于点 ,连接 , 为抛物线上一点,且位于线段 的上方,过 作 垂直 轴于点 , 交 于点 ,若 ,求点 坐标;
(3)已知点 , ,且无论 取何值,抛物线都经过定点 ,当 时,求抛物线的解析式.
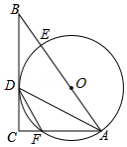
如图,在 中, , 平分 交 于点 , 为 上一点,经过点 、 的 分别交 、 于点 、 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径;
(3)求证: .