（本小题满分10分）
如图隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用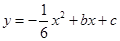
表示，且抛物线上的点C到OB的水平距离为3m，到地面OA的距离为
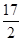m。
（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？
（3）在抛物线型拱璧上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？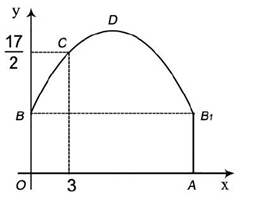
四川省第十二届运动会将于2014年8月18日在我市隆重开幕，根据大会组委会安排，某校接受了开幕式大型团体操表演任务．为此，学校需要采购一批演出服装，A、B两家制衣公司都愿成为这批服装的供应商．经了解：两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元．经洽谈协商：A公司给出的优惠条件是，全部服装按单价打七折，但校方需承担2200元的运费；B公司的优惠条件是男女装均按每套100元打八折，公司承担运费．另外根据大会组委会要求，参加演出的女生人数应是男生人数的2倍少100人，如果设参加演出的男生有x人．
（1）分别写出学校购买A、B两公司服装所付的总费用y1（元）和y2（元）与参演男生人数x之间的函数关系式；
（2）问：该学校购买哪家制衣公司的服装比较合算？请说明理由．
5月12日是母亲节，小明去花店买花送给母亲，挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花，已知康乃馨每支5元，兰花每支3元，小明只有30元，希望购买花的支数不少于7支，其中至少有一支是康乃馨．
（1）小明一共有多少种可能的购买方案？列出所有方案；
（2）如果小明先购买一张2元的祝福卡，再从（1）中任选一种方案购花，求他能实现购买愿望的概率．
某校七年级准备购买一批笔记本奖励优秀学生，在购买时发现，每本笔记本可以打九折，用360元钱购买的笔记本，打折后购买的数量比打折前多10本．
（1）求打折前每本笔记本的售价是多少元？
（2）由于考虑学生的需求不同，学校决定购买笔记本和笔袋共90件，笔袋每个原售价为6元，两种物品都打九折，若购买总金额不低于360元，且不超过365元，问有哪几种购买方案？
如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为3米，台阶AC的坡度为1：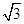
（即AB：BC=1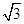：），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（侧倾器的高度忽略不计）．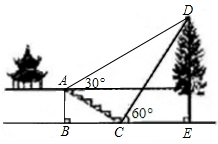
某校数学课题学习小组在“测量教学楼高度”的活动中，设计了以下两种方案：
| 课题 |
测量教学楼高度 |
|
| 方案 |
一 |
二 |
图示 |
 |
 |
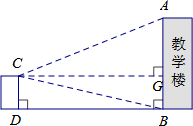| 测得数据 |
CD=6.9m，∠ACG=22°，∠BCG=13°， |
EF=10m，∠AEB=32°，∠AFB=43° |
| 参考数据 |
sin22°≈0.37，cos22°≈0.93， tan22°≈0.40 sin13°≈0.22，cos13°≈0.97 tan13°≈0.23 |
sin32°≈0.53，cos32°≈0.85，tan32°≈0.62 sin43°≈0.68，cos43°≈0.73，tan43°≈0.93 |
请你选择其中的一种方法，求教学楼的高度（结果保留整数）