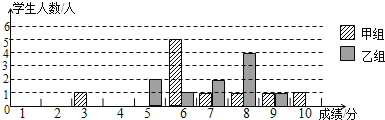
某校团委举办了一次“中国梦，我的梦”演讲比赛，满分10分，学生得分均为整数，成绩达6分以上为合格，达到9分以上（含9分）为优秀．这次竞赛中甲、乙两组学生成绩分布的条形统计图如下．
（1）补充完成下列的成绩统计分析表：
| 组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
| 甲 |
6．7 |
|
3．41 |
90% |
20% |
| 乙 |
|
7．5 |
|
80% |
10% |
（2）小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上表可知，小明是 组学生；（填“甲”或“乙”）
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．
一种产品的进价为40元，某公司在销售这种产品时，每年总开支为100万元（不含进价）．经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据：
| 销售单价x（元） |
50 |
60 |
70 |
80 |
| 年销售量y（万件） |
5．5 |
5 |
4．5 |
4 |
（1）求y关于x的函数关系式；
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围，使年利润不低于60万元．
如图，在同一平面内，两条平行高速公路l1和l2间有一条“Z”型道路连通，其中AB段与高速公路l1成30°角，长为20km；BC段与AB、CD段都垂直，长为10km，CD段长为30km，求两高速公路间的距离（结果保留根号）．
如图，矩形ABCD中，点E，F分别在AB，CD边上，连接CE、AF，∠DCE=∠BAF．试判断四边形AECF的形状并加以证明．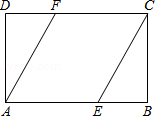
小明在学习反比例函数的图象时，他的老师要求同学们根据“探索一次函数y1=x+1的图象”的基本步骤，在纸上逐步探索函数y2=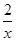
的图象，并且在黑板上写出4个点的坐标：A（
，
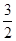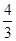），B（1，2），C（1，
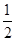），D（﹣2，﹣1）．
（1）在A、B、C、D四个点中，任取一个点，这个点既在直线y1=x+1又在双曲线y2=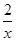上的概率是多少？
（2）小明从A、B、C、D四个点中任取两个点进行描点，求两点都落在双曲线y2=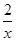上的概率．
（1）解方程：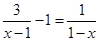
（2）解不等式组：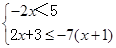
．