已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣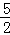 ).
).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.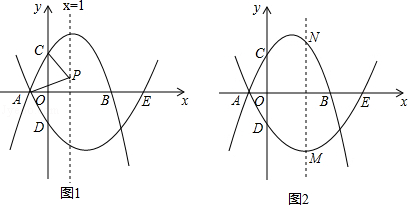
某中学举行了“班班有歌声”活动,某校比赛聘请了10位老师和10位学生担任评委,其中甲班的得分情况如统计图(表)所示.
老师评分统计表格:
| 评委序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 分数 |
94 |
96 |
93 |
91 |
X |
92 |
91 |
98 |
96 |
93 |
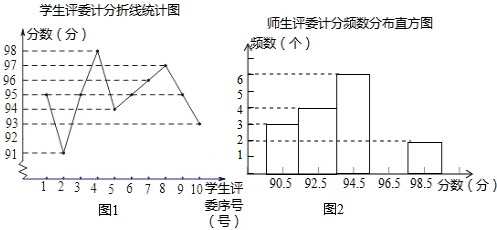
(1)在频数分布直方图中,自左向右第四组的频数为 ;
(2)学生评委计分的中位数是 分;
(3)计分办法规定:老师、学生评委的计分各去掉一个最高分、一个最低分,分别计算平均分,并且按老师、学生各占60%、40%的方法计算各班最后得分.已知甲班最后得分为94.4分,求统计表中x的值.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,∠1=∠2.
(1)求证:BE=DF;
(2)求证:AF∥CE.
已知x=2是关于x的一元二次方程x2+3x+m-2=0的一个根.
(1)求m的值及方程的另一个根;
(2)若7-x≥1+m(x-3),求x的取值范围.
已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:
甲:①连接OP,作OP的垂直平分线l,交OP于点A;
②以点A为圆心、OA为半径画弧、交⊙O于点M;
③作直线PM,则直线PM即为所求(如图1).
乙:①让直角三角板的一条直角边始终经过点P;
②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;
③作直线PM,则直线PM即为所求(如图2).
对于两人的作业,下列说法正确的是()
| A.甲对,乙不对 | B.甲不对,乙对 | C.两人都对 | D.两人都不对 |
如图,在矩形ABCD中,AD=8,AB=6,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时停止运动,点Q也随之停止,设点P,Q运动的时间是t秒(t>0)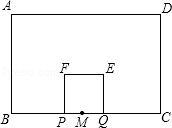
(1)用含t的代数式表示线段BQ的长;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,求S与t之间的函数关系式;
(3)连接AC,当正方形PQEF与△ADC重叠部分为三角形时,直接写出t的取值范围.