（广元）经统计分析．某市跨河大桥上的车流速度v（千米／时）是车流密度x（辆／千米）的函数，当桥上的车流密度达到220辆／千米的时候就造成交通堵塞．此时车流速度为0千米／时；当车流密度不超过20辆／千米，车流速度为80千米／时．研究表明：当
时，车流速度v是车流密度x的一次函数．
（1）求大桥上车流密度为100辆／千米时的车流速度；
（2）在某一交通时段．为使大桥上的车流速度大于60千米／时且小于80千米／时，应把大桥上的车流密度控制在什么范围内？
如图，已知：⊙O的直径AB与弦AC的夹角∠A=30°，AC＝CP．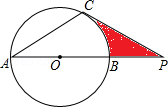
（1）求证：CP是⊙O的切线；
（2）若PC＝6，AB=4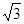
求图中阴影部分的面积．
解下列方程：（本题满分12分，每小题3分）
（1）
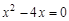
（2）
（配方法）
（3）
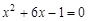
（4）
为了考察冰川融化的状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km 圆形考察区域，线段P1、P2是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年，冰川的边界线P1P2移动的距离为s（km），并且s与n（n为正整数）的关系是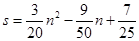
.以O为原点，建立如图所示的平面直角坐标系，其中P1、P2的坐标分别是（－4，9）、（－13，－3）.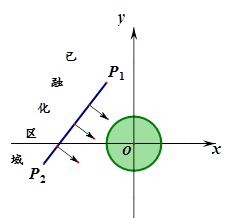
（1）求线段P1P2所在的直线对应的函数关系式；
（2）求冰川的边界线移动到考察区域所需要的最短时间.
如图，在矩形ABCD中，AB=16cm，BC=6cm，点P从点A出发沿AB以3cm/s的速度向点B移动，一直到达点B为止；同时，点Q从点C出发沿CD以2cm/s的速度向点D移动．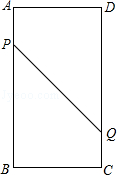
（1）经过多长时间P、Q两点之间的距离是10cm？
（2）连PD，经过多长时间△PQD是等腰三角形？
已知关于x的一元二次方程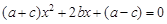
，其中a、b、c分别为△ABC三边的长．
（1）如果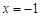
是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．