(南充)已知抛物线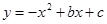 与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.
与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),与y轴相交于点C,顶点为P,对称轴为l:x=1.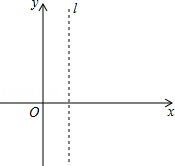
(1)求抛物线解析式.
(2)直线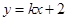 (
(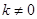 )与抛物线相交于两点M(
)与抛物线相交于两点M(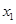 ,
,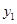 ),N(
),N(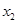 ,
,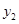 )(
)(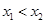 ),当
),当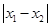 最小时,求抛物线与直线的交点M与N的坐标.
最小时,求抛物线与直线的交点M与N的坐标.
(3)首尾顺次连接点O、B、P、C构成多边形的周长为L,若线段OB在x轴上移动,求L最小值时点O,B移动后的坐标及L的最小值.
已知多项式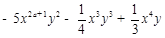 ⋅
⋅
(1)求多项式中各项的系数和次数;
(2)若多项式是7次多项式,求a的值.
求下列各式的值:(每小题5分,共15分)
(1)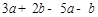 ,其中
,其中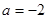 ,
,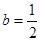 ;
;
(2)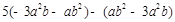 ,其中a=1,b=2;
,其中a=1,b=2;
(3)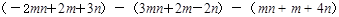 ,其中
,其中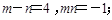
如图,在△ABC中,∠BAC=90°,AB=AC=6,D为BC的中点.
(1)若E、F分别是AB、AC上的点,且AE=CF,求证:△AED≌△CFD;
(2)当点F、E分别从C、A两点同时出发,以每秒1个单位长度的速度沿CA、AB运动,到点A、B时停止;设△DEF的面积为y,F点运动的时间为x,求y与x的函数关系式;
(3)在(2)的条件下,点F、E分别沿CA、AB的延长线继续运动,求此时y与x的函数关系式.
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,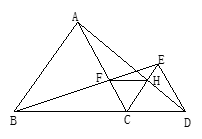
(1)求证:△BCE≌△ACD;
(2)求证:△CHF为等边三角形.
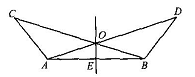
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.求证:OE垂直平分AB.