(达州)达州市某中学举行了“中国梦,中国好少年”演讲比赛,菲菲同学将选手成绩划分为A、B、C、D四个等级,绘制了两种不完整统计图.
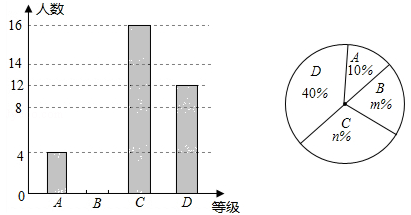
根据图中提供的信息,解答下列问题:
(1)参加演讲比赛的学生共有 人,扇形统计图中m= ,n= ,并把条形统计图补充完整.
(2)学校欲从A等级2名男生2名女生中随机选取两人,参加达州市举办的演讲比赛,请利用列表法或树状图,求A等级中一男一女参加比赛的概率.(男生分别用代码 A1、A2表示,女生分别用代码B1、B2表示)
(本小题满分8分)
如图, 为
为 的切线,
的切线, 为切点,
为切点, 交
交 于点
于点 ,求
,求 的度数.
的度数.
(本小题满分8分)
下图是由权威机构发布的,在1993年4月~2005年4月期间由中国经济状况指标之一中国经济预警指数绘制的图表.
(1)请你仔细阅读图
 表,可从图表中得出:我国
表,可从图表中得出:我国 经济发展过热的最高点出现在 年;我国经济发展过冷的最低点出现在 年.
经济发展过热的最高点出现在 年;我国经济发展过冷的最低点出现在 年.
(2)根据该图表提供的信息,请你简单描述我国从1993年4月到2005年4月经济发展状况,并预测2005年度中国经济发展的总体趋势将会怎样?
(本小题满分8分)
如图,已知在半圆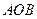 中,
中,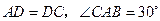 ,
,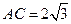 ,求
,求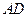 的长度.
的长度.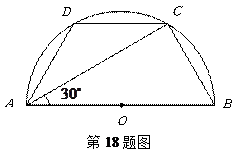
(本题共两小题,每小题6分,满分12分)
(1)解不等式组: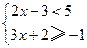
(2)因式分解: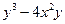
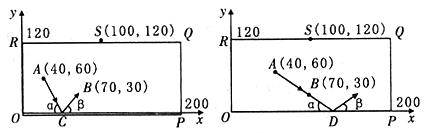
我们设想用电脑模 拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
(1)希望A球撞击桌边上C点后反弹,再击中B球,请给出一个算法,告知电脑怎样找到点C,并求出C点的坐标。
(2)设桌边RQ上有一球袋S(100,120),判定6号球B被从C点反弹出的白球撞击后能否直接落入球袋S中,(假定6号球被撞后速度足够大)。
(3)若用白球A直接击打6号球B,使6号球B撞击桌边OP上的D点后反弹,问6号球B从D点反弹后能否直接进入球袋Q中?(假定6号球被撞后速度足够大)