解方程组: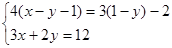
(1)如图,ΔABC中,∠ABC=50°,∠ACB=70°,D为边BC上一点(D与B、C不重合),连接AD,∠ADB的平分线所在直线分别交直线AB、AC于点E、F. 求证:2∠AED-∠CAD=170°;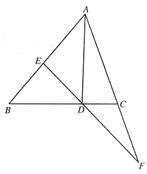
(2)若∠ABC=∠ACB=n°,且D为射线CB上一点,(1)中其他条件不变,请直接写出∠AED与∠CAD的数量关系.(用含n的代数式表示)
如图,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
(1)求ΔABC的面积;
(2)设点P在坐标轴上,且ΔABP与ΔABC的面积相等,求点P的坐标.
(1)如图,直线l 、l
、l 分别与直线l
分别与直线l 、l
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
(2)如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.
为了了解初一年级的学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了某校初一年级的学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图.

请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值和该校初一年级学生总数;
(2)求出活动时间为5天的学生人数,并补全条形统计图;
(3)如果某区初一年级的学生共有3000人,根据以上数据,试估计这3000人中“活动时间不少于4天”的百分比.