(达州)化简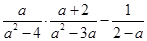 ,并求值,其中a与2、3构成△ABC的三边,且a为整数.
,并求值,其中a与2、3构成△ABC的三边,且a为整数.
某商场经销一种成本为每千克40元的水产品,经市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨价1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题.
(1)当销售单价定为每千克55元,计算月销售量和月销售利润;
(2)商场计划在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
如图,在直角坐标系中,一次函数y=kx+b的图象与反比例函数 的图象交于A(-2,1)、B(1,n)两点。
的图象交于A(-2,1)、B(1,n)两点。
(1)求m、n 的值;
(2)求上述反比例函数和一次函数的表达式;
(3)求△AOB的面积;
(4)当反比例函数大于一次函数时,x的取值范围。
如下图,路灯下,一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)试确定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树。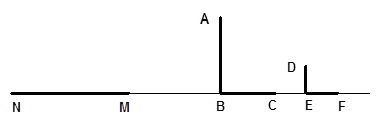
用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,请用列表法或树状图求乘积大于10的概率。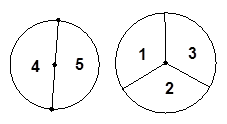
画出下列几何体的三视图