（成都）（本小题满分10分）已知AC，EC分别为四边形ABCD和EFCG的对角线，点E在△ABC内，∠CAE+∠CBE=90．
（1）如图①，当四边形ABCD和EFCG均为正方形时，连接BF．
i）求证：△CAE∽△CBF；
ii）若BE=1，AE=2，求CE的长；
（2）如图②，当四边形ABCD和EFCG均为矩形，且
时，若BE＝1，AE=2，CE=3，求k的值；
（3）如图③，当四边形ABCD和EFCG均为菱形，且∠DAB=∠GEF=45°时，设BE=m，AE=n，CE=p，试探究m，n，p三者之间满足的等量关系．（直接写出结果，不必写出解答过程）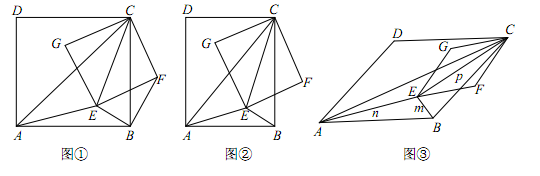
小李和小王设计了A、B两种游戏：
游戏A的规则：用四张数字分别为2、3、4、5的扑克牌，将扑克牌洗匀后背面朝上放在桌面上，第一次随机抽出一张牌记下数字后再原样放回，洗匀后再第二次随机抽出一张牌记下数字．若抽出的两张牌上数字之和为偶数，则小李获胜；若两数字之和为奇数，则小王获胜．
游戏B的规则：用四张数字分别为5、6、6、8的扑克牌，将牌洗匀后背面朝上放置在桌面上，小李先随机抽出一张牌，抽出的牌不放回，小王从剩下的牌中随机抽出一张牌．若小李抽出的牌面上的数字比小王的大，则小李获胜；否则，小王获胜．请你帮小王选择其中一种游戏，使他获胜的可能性较大，说明理由．
（本小题10分）云南省是我国花卉产业大省，一年四季都有大量鲜花销往全国各地，
花卉产
业已成为我省许多地区经济发展的重要项目．近年来某乡的花卉产值不断增加，2003年花卉的产值是640万元，2005年产值达到l000万元． (l）求2004年、2005年花卉产值的年平均增长率是多少？
(2）若2006年花卉产值继续稳步增长（即年增长率与前两年的年增长率相同）．那么请你估计2006年这个乡的花卉产值将达到多少万元？
（本小题9分）在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2个，黄球有1个，蓝球有1个. 现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由．
如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB＝30º，⊙O的半径为
cm，求弦CD的长.
（本小题9分）在
年植树节活动期间，某中学组织七年级
名学生、八年级
名学生、九年级
名学生参加义务植树活动，下图是根据植树情况绘制成的条形图（图1）
．请根据题
中提供的信息解答下列问题：
（1）参加植树的学生平均每人植树多少棵？
（2）图2是小明同学尚未绘制完成的各年级植树情况的扇形统计图，请你把它补充完整（要求标注圆心角度数）．