（攀枝花）如图，已知抛物线
与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，抛物线的对称轴与抛物线交于点P、与直线BC相交于点M，连接PB．
（1）求该抛物线的解析式；
（2）在（1）中位于第一象限内的抛物线上是否存在点D，使得△BCD的面积最大？若存在，求出D点坐标及△BCD面积的最大值；若不存在，请说明理由．
（3）在（1）中的抛物线上是否存在点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．
如图，抛物线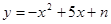
经过点A(1,0)，与y轴交于点B。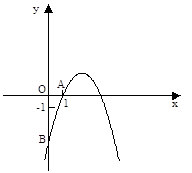
（1）求抛物线的解析式；
（2）P是y轴上一点，且△PAB是以AB为腰的等腰三角形，请直接写出P点坐标。
如图，在气象站台A的正西方向
的B处有一台风中心，该台风中心以每小时
的速度沿北偏东
的BD方向移动，在距离台风中心
内的地方都要受到其影响。
⑴台风中心在移动过程中，与气象台A的最短距离是多少？
⑵台风中心在移动过程中，气象台将受台风的影响，求台风影响气象台多长时间？
已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.
(1)求抛物线的解析式；
(2)求△MCB的面积S△MCB.
已知二次函数
的图象过点（-1，15），
求m的值；
若二次函数图象上有一点C，图象与x轴交于A、B两点，且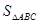
=3，求点C的坐标。
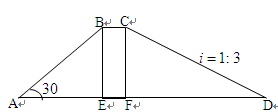
如图，水库大坝的横断面是梯形，坝顶宽BC=10米，坝高BE=CF=30米，斜坡AB的坡角∠A=30°，斜坡CD的坡度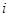
=1:3，求坝底宽AD的长.（结果保留根号）