（资阳）已知直线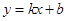
（
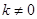）过点F（0，1），与抛物线
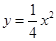相交于B、C两点．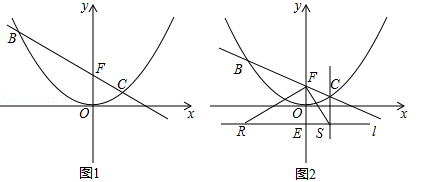
（1）如图1，当点C的横坐标为1时，求直线BC的解析式；
（2）在（1）的条件下，点M是直线BC上一动点，过点M作y轴的平行线，与抛物线交于点D，是否存在这样的点M，使得以M、D、O、F为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由；
（3）如图2，设B（m，n）（m＜0），过点E（0，﹣1）的直线l∥x轴，BR⊥l于R，CS⊥l于S，连接FR、FS．试判断△RFS的形状，并说明理由．
为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1.6米，标杆为3.1米，且BC=1米，CD=5米，请你根据所给出的数据求树高ED.
已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：
| x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
8 |
3 |
0 |
-1 |
0 |
3 |
… |
(1) 求该二次函数的解析式；
(2) 当x为何值时，y有最小值，最小值是多少？
(3)
若A（m,y1）,B(m+2, y2)两点都在该函数的图象上，计算当m取何值时，
在平面直角坐标系xoy中，已知
三个顶点的坐标分别为
⑴ 画出
；⑵ 画出
绕点
顺时针旋转
后得到的
，并求出
的长.
如图，在△ABC中，点D在边AB上，满足且∠ACD =∠ABC，若AC = 2，AD =1，求DB
的长.
已知排水管的截面为如图所示的圆
,半径为10，圆心到水面的距离是6，求水面宽
.